Un problème proposé par Pierre Arnoux aux élèves de 5e de l'atelier MeJ du collège Simone Veil.

(en complément à cet article : une séance construite est testée en classe de seconde ( pdf ; odt ) par Thomas Blanc et Bruno Mifsud)

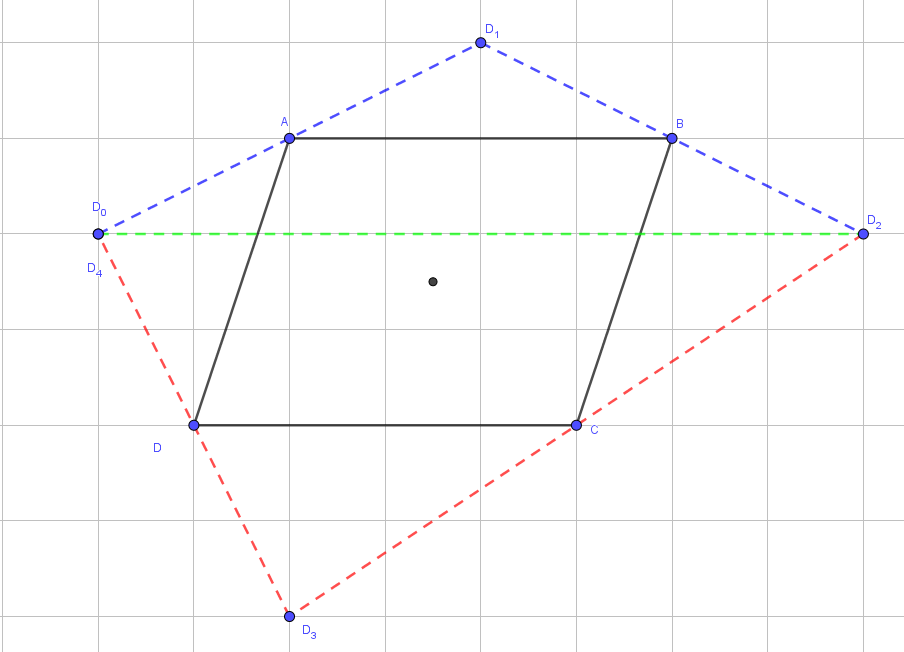
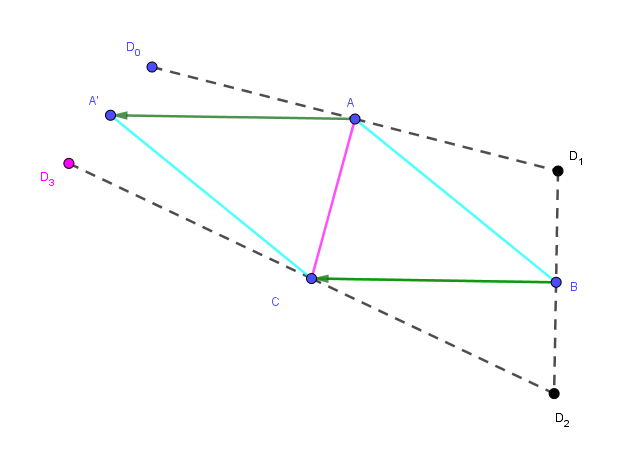
"On considère un polygone et un point D₀ extérieur au polygone.

1. On construit le symétrique D₁ du point D₀ par rapport à un des deux sommets du polygone les plus proches du point D₀.

2. On construit le point D₂ symétrique du point D₁ par rapport au "sommet suivant" c’est-à-dire le plus proche de D₁ et différent du précédent sommet utilisé.

3. On continue indéfiniment…

À quelle.s condition.s existe-t-il un point D_i qui soit superposé au point D₀ ?"

A venir sur cette page : les propositions et démonstrations des élèves et des membres du labo